Optically and magnetically active point defect centers in semiconductors may realize as quantum bit candidates for quantum computing. One of the exemplary and most studied centers is the nitrogen vacancy (NV) center in diamond. This system exhibits triplet electronic spin that can be coherently manipulated and can be read out as a qubit even at room temperature by optical means. Over the years, a plethora of non-characterized defect centers were created in various semiconductor materials. Therefore, among those there might be ones that possess even better properties than that of NV for quantum technologies. However, the many properties of these defect centers, optical centers, electron paramagnetic resonance (EPR) centers are left unknown in experimental measurements. 

 

Additionally, there are various technological challenges to overcome for defect-based qubits and quantum emitters that still limit the defect qubit applications “en masse”. Mainly, these challenges are related to the loss of coherence within qubits which is especially important when the qubits are entangled together as a solid-state spin qubit register. For example, magnetic dipole-dipole interaction between the qubit and neighboring spins of other defects or nuclei can be the source of such relaxation. Additional unavoidable decoherence channels may appear due to thermal phonons of the host material known as "spin-lattice" Orbach relaxation. Interactions with phonon are not limited to spin-phonon terms as the much stronger electron-phonon interaction (for example within the Huang-Rhys approximation) may impose severe limitations on the applicapibility of defects. The PhD student would emerge in such theories and unravel the applicapibility of ab-initio calculations on first and second order (Raman) phonon interactions which terms govern the coherence properties of defect qubits. 

 

Therefore, the PhD student would unravel the physical nature of these defect centers embedded in diamond and other semiconductors (silicon, silicon-carbide, 2 dimensional boron-nitride, etc.) by means of density functional theory (DFT) calculations on the electronic structure within and beyond the Born-Oppenheimer approximation. The research will be devoted to the characterization of defect centers by providing insight into their electronic structure and thus predict their optically excited states and quantify their radiative and non-radiative relaxation processes. Additionally, other interactions may also govern the physical processes of defect centers: spin-orbit coupling, hyperfine coupling, magnetic spin-spin interaction, nuclear quadrupole interaction, electron-phonon and spin-phonon coupling, various forms of electron-phonon coupling such as Jahn-Teller instability or Huang-Rhys theory – all of them may be a key element for actual real-world qubit realizations utilizing defects. Yet, not all of these physical properties can be measured directly by experimental methods thus suggesting the need of theoretial simulations from first principles to unravel such "hidden" properties.

 

Therefore, the results may contribute for realization of qubits in solids or greatly improve the already known defect centers by optimization. Additionally, the PhD student may develop and improve the ab-initio codes and apply them on the selected defect centers of the Research Topic that may approximate the relaxation and coherence times directly from first principles. These studies will be carried out in close collaboration with domestic and international partners (Ulm University or Max Planck Institute for Polymer Research for example). The ab-initio calculations will be run on the computer cluster. The research group that research group is simultaneously split between BME “FA” building and Wigner RCP.

 

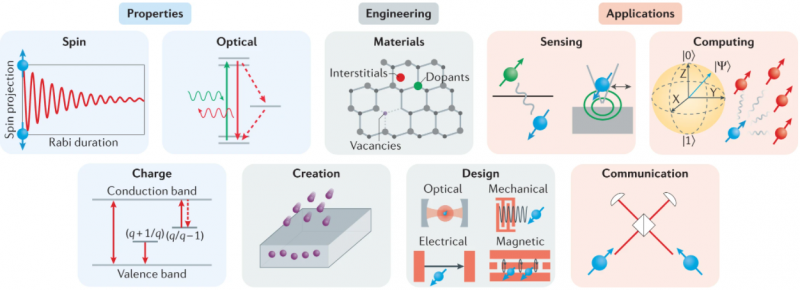Illustration of key concepts in the field, highlighting the three major defect properties (spin, optical and charge) in the blue panels, engineering considerations (materials, creation and design) in the grey panels and the three major quantum applications (sensing, communication and computing) in the red panels. Ref. Wolfowicz, G., Heremans, F.J., Anderson, C.P. et al. Quantum guidelines for solid-state spin defects. Nat Rev Mater 6, 906–925 (2021). https://doi.org/10.1038/s41578-021-00306-y

 

 

 

Requirements: 

- Keen interest for physics. Curiosity for theoretical derivations on a piece sheet of paper and their realization by means of model simulations on massively parallell computers.

- Excellent knowledge of quantum mechanics. Preferentially, solid knowledge of solid state physics, condensed matter physics or quantum chemistry. (for example: hydrogen atom with n, l, ml quantum numbers, origin of spin-orbit coupling, Periodic table, Fermi's golden rule, Many-body formalism with ladder operators, group theory, GW, BSE, Hartree-Fock equations etc.)

- Optional: Linux shell or terminals. Basic/advanced programmig or scripting skills. There is a possibility that the subject of the PhD may additionally lead to development of ab-initio codes (VASP, Quantum Espresso, etc.) that are written in high level Fortran, C, C++, python.